La funzione $f$ deve essere abbastanza regolare per avere la derivazione sotto il segno di integrale: più precisamente $f$ deve essere sommabile rispetto ad $x$ per ogni $t$, per ogni $x$ la funzione $f$ deve essere derivabile rispetto a $t$ ed infine deve esistere una funzione $g$ sommabile che dipende solo da $x$ tale per cui si.. Il teorema di derivazione per le serie di potenze ci dice che una serie di potenze e la sua serie derivata hanno lo stesso raggio di convergenza, quindi studiare l'una o l'altra è praticamente la stessa cosa! Inoltre, nel secondo punto del suo enunciato, ci permette di portare il segno di derivata dentro il segno di sommatoria, ovvero, se

Derivata Prima di una Funzione in un suo Punto utilizzando la Definizione YouTube

DERIVATA di un PRODOTTO e di un QUOZIENTE YouTube

Teorema del passaggio al limite sotto il segno di derivata Appunti di Analisi Matematica II

PPT LA DERIVATA DI UNA FUNZIONE PowerPoint Presentation, free download ID2434290

SEGNO DELLA DERIVATA E MONOTONIA DI UNA FUNZIONE Andrea il Matematico

SEGNO DELLA DERIVATA E MONOTONIA DI UNA FUNZIONE Andrea il Matematico

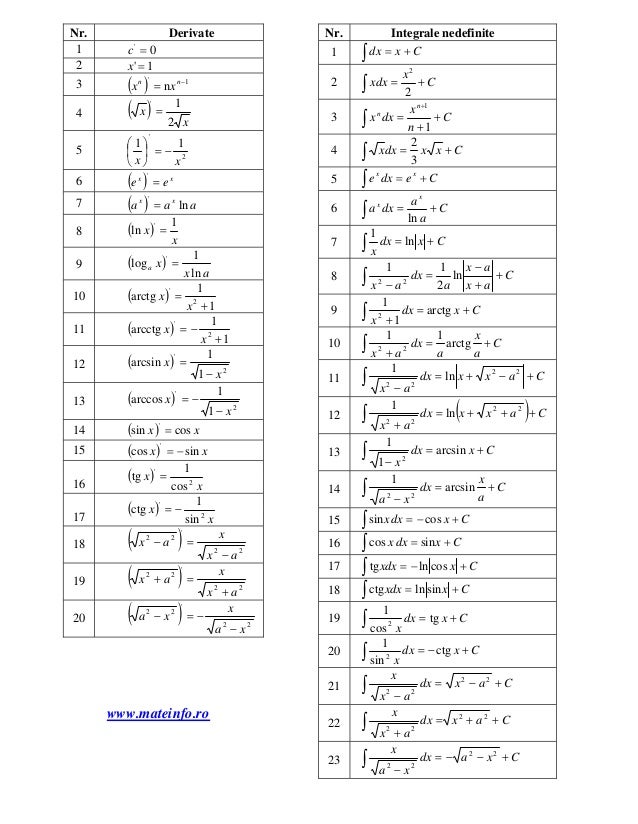
tabel derivate si integrale

Studio di funzione con derivata prima difficile studiare il segno della derivata prima

PPT CONCETTO DI DERIVATA PowerPoint Presentation, free download ID3215560

PUNTI STAZIONARI E SEGNO DELLA DERIVATA PRIMA massimi e minimi relativi e possibili flessi

Tabella Derivate Funzioni Elementari

Teorema passaggio al limite sotto il segno della derivata Algo and Math

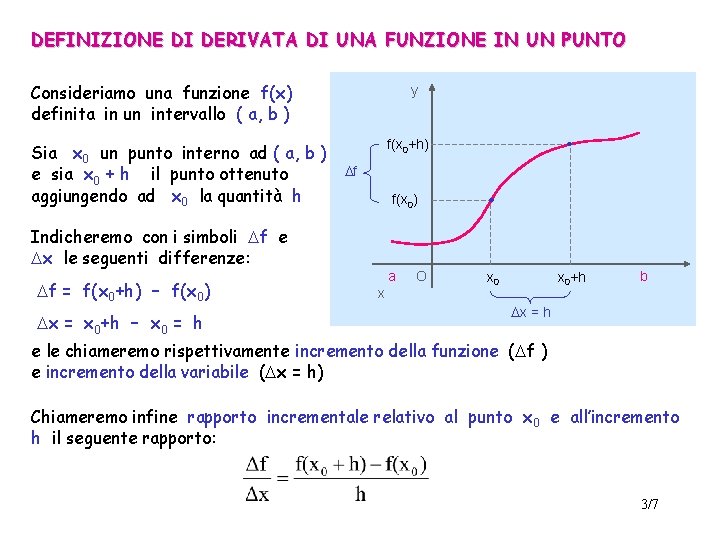
DERIVATA DI UNA FUNZIONE Concetti introduttivi Definizione di

Studio del segno Matematica Dolce

studio del segno della derivata Mappa concettuale

Derivataquoziente YouTube

Teorema passaggio al limite sotto il segno della derivata Algo and Math

Significato geometrico di derivata come coefficiente angolare Studenti.it

Derivate analisi Derivate derivate delle funzioni elementari dove k è una costante regole di

Derivata di una Funzione Integrale YouTube

Derivata sotto il segno di integrale 23 8. Integrale di Riemann e integrale di Lebesgue 24 3. CHAPTER 1 Introduzione alla teoria della misura 1. Misure esterne e misure su ˙-algebre. Criterio di Carath eodory In questa sezione introduciamo le de nizioni di misura esterna, di ˙-algebra, e. Derivazione sotto il segno dell'integrale. Lemma 1. Sia. R. = [a; b] (C; D) un rettangolo in. R2. Sia. f. : R ! una funzione tale che: per ogni. ssato. x. 2. [a; b] la funzione. f(x; ) : (C; D) ! R. e derivabile sull'intervallo. (C; D); in un punto. y. 2. (C; D) indicheremo la sua derivata con. @yf(x; y); la funzione. @yf. : [a; b]